Hemos visto que los conjuntos agrupan elementos como si fuesen bolsas, sin mantener información acerca del orden de los elementos que contienen.

Supongamos que tenemos 3 vasos dispuestos en una linea, con alturas 3, 1 y 2 unidades de izquierda a derecha. Una forma de representar el orden relativo de los vasos es a través del conjunto $O_{312} = \{ \{3\}, \{3, 1\}, \{ 3, 1, 2\} \}$. Si los vasos estuvieran en el orden 1, 2, 3 el conjunto sería $O_{123} = \{ \{1 \}, \{ 1, 2 \}, \{ 1,2,3\} \}$, agregamos un subconjunto por cada prefijo de vasos. En esta construcción, para encontrar el $i$-ésimo elemento en la linea, tenemos que buscar el subconjunto que contiene $i$ elementos y restarle el subconjunto de $i-1$ elementos.

Otra forma de representar el orden de elementos 3, 1, 2, es creando un conjunto de pares $I_{312}=\{(1,3), (2,1), (3,2)\}$. El par $(1, 3)$ significa que el elemento en la posición $1$ es $3$. Una representación similar es $P_{312}=\{ (1,2), (2,3), (3,1) \}$, el par $(1,2)$ significa mover el vaso $1$ a la posición $2$, el par $(2,3)$ mover el vaso $2$ a la posición $3$ y $(3,1)$ mover el vaso $3$ a la posición $1$. En ambas representaciones estamos asignando a cada entero desde $1$ hasta $3$ un entero diferente también desde $1$ hasta $3$. Esto es lo mismo que una función biyectiva del conjunto $\{ 1, 2, 3\}$ hacia el mismo conjunto $\{ 1,2,3\}$. Por supuesto, es necesario definir qué es un par (ordenado) ya que $(x,y) \neq (y,x)$.

Definiremos a las permutaciones como instrucciones de movimiento que se aplican sobre una secuencia para cambiar el orden de sus elementos. Denotemos a una permutación de $n$ elementos usando una tupla $p=(p_1, p_2, \ldots, p_n)$, el $i$-ésimo elemento de la permutación significa que el elemento $i$ debe moverse a la posición $p_i$. Por ejemplo la permutación $(4, 2, 1 ,3)$, representa $4$ vasos ordenados en una línea con alturas $3, 2, 4, 1$. La permutación actúa como si fuese una función $p(1) = 4$, $p(2)=2$, $p(3)=1$, $p(4)=3$.

La composición de funciones $f \circ g (x) = f(g(x))$ también está definida para permutaciones. Si $f=(4,2,1,3)$ y $g=(1,4,2,3)$, entonces $f \circ g = (4, 3, 2, 1)$. Primero se aplica los movimientos de la permutación $g$ y luego los de $f$. La permutación $g$ mueve el elemento $1$ a la posición $1$, y luego $f$ mueve el elemento de la posición $1$ a la posición $4$. Similarmente, $g$ mueve el elemento $2$ a la posición $4$, y luego $f$ mueve el elemento $4$ a la posición $3$.

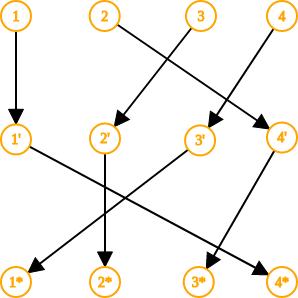
Sea $S_n$ el conjunto de todas las permutaciones de $n$ elementos, junto con la operacion composición ($\circ$) obtenemos un grupo. El elemento identidad es $e=(1,2, 3, \ldots n)$, esta permutación hace que cada elemento se quede en su misma posición. Las permutaciones también tienen su inversa, si en la permutación $p$ el elemento $x$ se mueve a la posición $y$, en la permutación inversa $p^{-1}$, el elemento $y$ debe regresar a la posición $x$. Similarmente observando cómo se mueven los elementos, se puede demostrar que la operación de composición es asociativa.

¿Cuántos elementos tiene $S_n$?

$S_3= \{ (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1) \}$

Construyamos todas las permutaciones de $S_n$. El primer elemento de la permutación puede ser cualquiera de los enteros desde $1$ hasta $n$, por tanto hay $n$ posibilidades. Una vez decidido el valor del primer elemento, tenemos que llenar las siguientes $n-1$ posiciones usando $n-1$ números distintos, lo cual es equivalente a contar el número de elementos de $S_{n-1}$.

Denotemos por $n!$ (se lee $n$ factorial) a la cantidad de elementos de $S_n$. La recurrencia del parrafo anterior es $n! = n \cdot (n-1)!$. Hay sólo una forma de ordenar una secuencia de un elemento, por tanto $1!=1$. Si expandimos la recurrencia, obtenemos $n!=n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 1$. Los 10 primeros factoriales son 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800.

Para calcular $n!$ tenemos que realizar un número de multiplicaciones proporcional a $n$. En general, no hay una forma de encontrar los factoriales exáctamente sin recorrer todos los números de $1$ a $n$. Sin embargo, hay ciertas aproximaciones, por ejemplo los factoriales crecen más rápido que $2^n$ y mas lento que $n^n$. Stirling encontró una aproximación más precisa: $n! \approx \sqrt{2 \pi n} \cdot (\frac{n}{e})^n$