Muchos de los procesos naturales contienen una parte aleatoria, algo hace que el resultado de nuestras observaciones no siempre sea el mismo. Por ejemplo, si lanzamos una moneda al aire, a veces cae cara y a veces sello. Podríamos pensar que si conocemos exactamente todas las caraterísticas geometricas de la moneda, el impulso inicial, y la resistencia del viento, entonces es posible calcular con precisión cual será el resultado. En muchas situaciones el número de variables a considerar es muy grande y en otros casos, pequeños cambios en las condiciones iniciales hacen que los resultados sean muy diferentes.

Las teorías que plantean la posibilidad de determinar con exactitud el resultado final dado las condiciones iniciales son llamadas deterministas. Laplace pensaba que si una inteligencia superior (Dios?) conociese las posiciones y fuerzas sobre cada partícula del universo, y tuviese el suficiente poder computacional, entonces podría determinar con exactitud el futuro. ¿Donde queda nuestro libre albedrío?

Se han descubierto fenómenos que aparentemente rompen el determinismo. Dadas las (mismas) condiciones iniciales, cada vez que hace una obervación se obtienen resultados diferentes. Para explicar tales fenómenos, se han desarrollado teorías capaces de determinar con qué probabilidad se obtienen los posibles resultados, es decir en que proporción se obtiene cada resultado respecto a los otros.

Supongamos que realizamos un experimento aleatorio, por ejemplo lanzar un dado y observar el número en la cara superior. El conjunto de todos los resultados posibles es llamado espacio muestral, en nuestro caso hay 6 posibilidades. Si repetimos el experimento aleatorio un número grande de veces (digamos $N$), podemos contar el número de veces que el dado cayó 1, el número de veces que cayó 2, ..., el número de veces que cayó 6. Sea $C_x$ el número de veces que el dado cayó $x$, definiremos la probabilidad de que el dado caiga $x$ como $P_x = C_x/N$. Es decir, la probabilidad representa la proporción del número de veces que ocurre cada resultado. Observa que $C_1+C_2+ \ldots +C_6 = N$, la consecuencia es que la suma de probabilidades de todos los eventos del espacio muestral suma $1$. Si consideramos que el dado es ideal, no existe una cara especial (todas son iguales), por lo que esperaríamos obtener $C_1=C_2=...=C_6=1/6$. Podemos tomar ciertos elementos de interés del espacio muestral, por ejemplo podemos tomar todas los casos en los que el dado cayó un numero mayor a 3, la probabilidad de que ocurra esto es $(C_4+C_5+C_6)/N$. A estos subconjuntos del espacio muestral se les denomina eventos

A veces el espacio muestral no es discreto, y es necesario extender el enfoque frecuentista (el conteo de cada posible resultado). Por ejemplo supongamos que tenemos un círculo de radio $R$ inscrito en un cuadrado. Supongamos que tomamos un punto aleatorio dentro del cuadrado. ¿Cuál es la probabilidad que el punto caiga dentro del círculo?

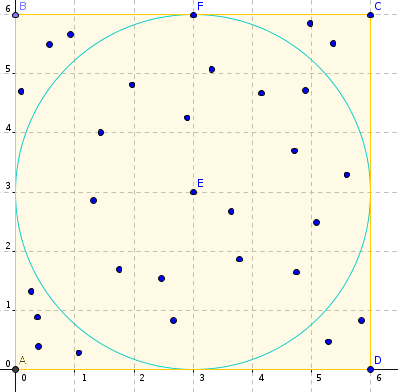
Podemos hacer llover $N$ puntos aleatoriamente, y contar el número de puntos $C$ que caen dentro del círculo, la probabilidad es $P=C/N$. Supongamos que dividmos a la figura usando una malla muy fina de cuadraditos. Cada cuadradito en la malla tiene la misma probabilidad de que le llueva un punto. La forma de medir el número de cuadraditos dentro de una figura es el área, por tanto también podemos calcular la probabilidad dividiendo el área del circulo entre el área del cuadrado $P=\pi \cdot R^2 / 4 \cdot R^2$. Las computadoras pueden fácilmente hacer la simulación generando un montón de puntos y contando cuántos caen dentro del círculo, si igualamos las dos ecuaciones anteriores, ¡obtenemos un método para calcular $\pi$! Este algoritmo es llamado método de Montecarlo, es uno de los pocos métodos para calcular áreas que se puede extender a más dimensiones.