Matemática 1 - Análisis
habilmente.xyz
¿Qué número sigue? (5 pts)
1, 3, 5, 9, 17, 31, ?
Solución9 = 1 + 3 + 5
17 = 9 + 5 + 3
31 = 17 + 9 + 5
El rey esta apurado (5 pts)
En la siguiente figura se muestra un rey en la casilla c2, y un círculo en f7
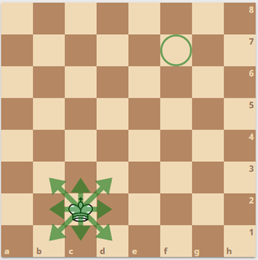
El rey se mueve como en el ajedrez. En un movimiento, puede moverse a cualquiera de las casillas adyacentes que comparta al menos un vértice con la casilla en la que está actualmente
¿Cuál es el mínimo número de movimientos necesarios para que el rey llegue hasta el círculo?
SoluciónEl rey debe dar 3 pasos en horizontal y 5 en vertical. Para acortar la distancia, al rey le conviene dar la máxima cantidad de pasos en diagonal. Un paso en diagonal es equivalente a dar un paso en horizontal seguido de uno en vertical. Por lo tanto, despues de 3 pasos en diagonal, solo le faltará dar dos pasos más en vertical. En matemática esta métrica es conocida como Distancia de Chebyshev.
La estrella de Da Vinci (10 pts)
Leonardo vive en un país de 5 ciudades (enumeradas desde 1 hasta 5). Por cada par de ciudades diferentes, existe una carretera que las conecta. La figura de abajo muestra un mapa del pais.
Leonardo está en la ciudad 1 y quiere viajar hasta la ciudad 4. Durante su viaje, Leonardo no quiere visitar la misma ciudad más de una vez.
Leonardo puede realizar su viaje de varias formas. Por ejemplo, puede ir directo hasta la ciudad 4, o seguir otra secuencia más larga como 1, 2, 5, 4.
¿De cuántas formas diferentes puede Leonardo realizar su viaje?

- Secuencias de longitud 2: Una única forma, ir directo desde 1 hasta 4
- Secuencias de longitud 3: Tenemos que seleccionar una ciudad de paso, la cual puede ser 2, 3 o 5. Por tanto hay tres formas: $(1, 2, 4), (1, 3, 4), (1, 5, 4)$
- Secuencias de longitud 4: Hay 3 posibilidades para la primera ciudad de paso, y 2 para la siguiente (no podemos repetir la misma ciudad). Por tanto hay 3*2 = 6 formas
- Secuencias de longitud 5: Las 3 ciudades restantes tienen que ser de paso, el número de permutaciones es 3! = 6
Rectángulos e histogramas (5 pts)
La figura de abajo muestra una región poligonal azul (histograma).
Un rectángulo es bueno si cumple las siguientes restricciones:
- Sus lados son paralelos a los ejes coordenados
- Sus vertices tienen coordenadas enteras
- El rectángulo esta dentro del histograma (inscrito)
¿Cuántos rectángulos buenos existen con área máxima?
Más formalmente, sea S el conjunto de todas las áreas de rectángulos buenos, y sea A el máximo elemento de S (el número más grande). Calcula el número de rectangulos buenos con área igual a A.
SoluciónAlgunos participantes buscaban los cuadrados multiplicando base x altura, es más natural usar la definición de área i.e el número de cuadraditos de 1 x 1 que entran en la figura
La siguiente figura muestra uno de los rectángulos buenos de área máxima (8 cuadraditos)

Jugando con piedritas 2 (5 pts)
Samuel y Feliza estan jugando con piedritas. Hay dos filas, la primera con 6 piedritas y la segunda con 4.
Samuel y Feliza alternan turnos, Samuel mueve primero, luego Feliza y así sucesivamente.
En cada turno el jugador que le toca puede seleccionar una de las filas y quitar un número positivo (mayor a cero) de piedritas.
El jugador que no pueda sacar piedritas pierde.
Antes de empezar el juego, Feliza eliminará algunas de las piedritas de cualquiera de las filas (quizas de ambas filas). Para que Samuel no sospeche, Feliza dejará al menos una piedrita en cada fila.
¿De cuántas formas puede Feliza eliminar las piedritas para garantizar su victoria?
3 Participantes obtuvieron score perfecto durante la primera semana de la competencia!
| Usuario | Puntos |
|---|---|
| Juliaruiz1 | 30 |
| wil | 30 |
| AILE | 30 |

