Alfa Omega en Zulema Arce primero B
habilmente.xyz
Niños de 6 años del primero B a cargo de la profesora Gretna Ivonne vienen reforzando su aprendizaje de lectura usando la aplicacion web Alfa Omega de habilmente.xyz

Niños de 6 años del primero B a cargo de la profesora Gretna Ivonne vienen reforzando su aprendizaje de lectura usando la aplicacion web Alfa Omega de habilmente.xyz
Alfa Omega una aplicacion web que escucha y pronuncia ideal para aprender a leer
Hemos visto que los conjuntos agrupan elementos como si fuesen bolsas, sin mantener información acerca del orden de los elementos que contienen.
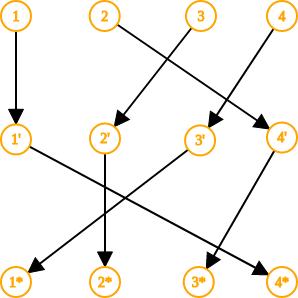
Supongamos que tenemos 3 vasos dispuestos en una linea, con alturas 3, 1 y 2 unidades de izquierda a derecha. Una forma de representar el orden relativo de los vasos es a través del conjunto $O_{312} = \{ \{3\}, \{3, 1\}, \{ 3, 1, 2\} \}$. Si los vasos estuvieran en el orden 1, 2, 3 el conjunto sería $O_{123} = \{ \{1 \}, \{ 1, 2 \}, \{ 1,2,3\} \}$, agregamos un subconjunto por cada prefijo de vasos. En esta construcción, para encontrar el $i$-ésimo elemento en la linea, tenemos que buscar el subconjunto que contiene $i$ elementos y restarle el subconjunto de $i-1$ elementos.
Otra forma de representar el orden de elementos 3, 1, 2, es creando un conjunto de pares $I_{312}=\{(1,3), (2,1), (3,2)\}$. El par $(1, 3)$ significa que el elemento en la posición $1$ es $3$. Una representación similar es $P_{312}=\{ (1,2), (2,3), (3,1) \}$, el par $(1,2)$ significa mover el vaso $1$ a la posición $2$, el par $(2,3)$ mover el vaso $2$ a la posición $3$ y $(3,1)$ mover el vaso $3$ a la posición $1$. En ambas representaciones estamos asignando a cada entero desde $1$ hasta $3$ un entero diferente también desde $1$ hasta $3$. Esto es lo mismo que una función biyectiva del conjunto $\{ 1, 2, 3\}$ hacia el mismo conjunto $\{ 1,2,3\}$. Por supuesto, es necesario definir qué es un par (ordenado) ya que $(x,y) \neq (y,x)$.
Definiremos a las permutaciones como instrucciones de movimiento que se aplican sobre una secuencia para cambiar el orden de sus elementos. Denotemos a una permutación de $n$ elementos usando una tupla $p=(p_1, p_2, \ldots, p_n)$, el $i$-ésimo elemento de la permutación significa que el elemento $i$ debe moverse a la posición $p_i$. Por ejemplo la permutación $(4, 2, 1 ,3)$, representa $4$ vasos ordenados en una línea con alturas $3, 2, 4, 1$. La permutación actúa como si fuese una función $p(1) = 4$, $p(2)=2$, $p(3)=1$, $p(4)=3$.
La composición de funciones $f \circ g (x) = f(g(x))$ también está definida para permutaciones. Si $f=(4,2,1,3)$ y $g=(1,4,2,3)$, entonces $f \circ g = (4, 3, 2, 1)$. Primero se aplica los movimientos de la permutación $g$ y luego los de $f$. La permutación $g$ mueve el elemento $1$ a la posición $1$, y luego $f$ mueve el elemento de la posición $1$ a la posición $4$. Similarmente, $g$ mueve el elemento $2$ a la posición $4$, y luego $f$ mueve el elemento $4$ a la posición $3$.
Sea $S_n$ el conjunto de todas las permutaciones de $n$ elementos, junto con la operacion composición ($\circ$) obtenemos un grupo. El elemento identidad es $e=(1,2, 3, \ldots n)$, esta permutación hace que cada elemento se quede en su misma posición. Las permutaciones también tienen su inversa, si en la permutación $p$ el elemento $x$ se mueve a la posición $y$, en la permutación inversa $p^{-1}$, el elemento $y$ debe regresar a la posición $x$. Similarmente observando cómo se mueven los elementos, se puede demostrar que la operación de composición es asociativa.
¿Cuántos elementos tiene $S_n$?
$S_3= \{ (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1) \}$
Construyamos todas las permutaciones de $S_n$. El primer elemento de la permutación puede ser cualquiera de los enteros desde $1$ hasta $n$, por tanto hay $n$ posibilidades. Una vez decidido el valor del primer elemento, tenemos que llenar las siguientes $n-1$ posiciones usando $n-1$ números distintos, lo cual es equivalente a contar el número de elementos de $S_{n-1}$.
Denotemos por $n!$ (se lee $n$ factorial) a la cantidad de elementos de $S_n$. La recurrencia del parrafo anterior es $n! = n \cdot (n-1)!$. Hay sólo una forma de ordenar una secuencia de un elemento, por tanto $1!=1$. Si expandimos la recurrencia, obtenemos $n!=n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 1$. Los 10 primeros factoriales son 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800.
Para calcular $n!$ tenemos que realizar un número de multiplicaciones proporcional a $n$. En general, no hay una forma de encontrar los factoriales exáctamente sin recorrer todos los números de $1$ a $n$. Sin embargo, hay ciertas aproximaciones, por ejemplo los factoriales crecen más rápido que $2^n$ y mas lento que $n^n$. Stirling encontró una aproximación más precisa: $n! \approx \sqrt{2 \pi n} \cdot (\frac{n}{e})^n$
El siguiente diagrama muestra una matriz de $4$ filas y $4$ columnas. Enumeremos las filas de arriba hacia abajo, y a las columnas de izquierda a derecha. Denotaremos la celda que está en la fila $r$ y columna $c$ usando un par ordenado $(r, c)$. Al igual que en el plano cartesiano, empezaremos la enumeración empezando desde $0$. Por ejemplo, la celda amarilla está codificada por el par $(1, 2)$.
| 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 |
| 1 | 3 | 6 | 10 |
| 1 | 4 | 10 | 20 |
Hay hay un ratón en la celda $(0, 0)$ que quiere viajar hasta la celda $(3, 3)$. En un movimiento, el ratón puede decidir moverse una columna hacia la derecha, o una fila hacia abajo. Más formalmente, si el ratón está en la celda $(r, c)$, este puede moverse hacia la celda $(r, c + 1)$ o hacia $(r + 1, c)$, siempre que tal celda exista. Por ejemplo, si el ratón está en la celda amarilla $(1, 2)$ entonces puede moverse hacia la derecha $(1, 3)$ o hacia abajo $(2,2)$.
¿De cuántas formas puede realizar su viaje el ratón?
Observa que hay una sola forma de llegar a las celdas de la primera fila (solo podemos llegar a tales celdas moviéndonos siempre hacia la derecha). Similarmente, hay una única forma de llegar a las celdas de la primera columna (solo podemos llegar a tales celdas moviéndonos siempre hacia abajo).
Denotemos por $F(r, c)$ al número de formas en las que el ratón puede llegar a la celda $(r,c)$. Con esta notación, la afirmación del parrafo anterior se resume a $F(0, x) = F(x, 0) = 1$ para cualquier $x$ válido.
Para llegar a la celda celeste $(1, 1)$, anteriormente el ratón debió estar una celda hacia la izquierda $(1, 0)$ o una celda hacia arriba $(0, 1)$. Por tanto $F(1, 1) = F(1, 0) + F(0, 1) = 1 + 1 = 2$. Similarmente con la celda amarilla $F(1, 2) = F(1, 1) + F(0, 2) = 2 + 1 = 3$. Con esta idea podemos calcular el número de formas en las que puede el ratón llegar a cada celda.
Más generalmente, la única forma en la que el ratón puede llegar a la celda $(x, y)$ es dando un paso hacia abajo desde $(x-1, y)$ o dando un paso a la derecha desde $(x, y - 1)$. Por tanto, $F(x,y) = F(x-1, y) + F(x, y-1)$. A este tipo de ecuaciones se les llama recurrencias, calculamos el valor de cierta función a partir de valores calculados anteriormente.
Los movimientos del ratón pueden ser codificados con una cadena de 6 caracteres, por ejemplo DAADDA significa que primero el ratón se movió hacia la derecha, después dos veces hacia abajo, luego dos veces hacia la derecha y finalmente una vez hacia abajo.
Cualquier cadena de seis letras que tenga $3$ letras D y $3$ letras A (en cualquier orden) representa una forma de movimiento para el ratón. De las seis posiciones disponibles, tenemos que seleccionar 3 en las cuales pondremos caracteres D, y en el resto caracteres A. El número de formas de realizar esto es $\binom{6}{ 3}$.
Más generalmente, si el ratón quiere llegar a la celda $(r,c)$, entonces tiene que dar $r$ pasos hacia abajo y $c$ hacia la derecha, por tanto su movimiento está codificado por una cadena de $r+c$ letras, de las cuales tenemos que escoger $r$ posiciones para poner la letra A y en las $c$ posiciones restantes la letra D. Esto se puede hacer de $\binom{r+c}{r}$ formas.
Se observa que hay una relación entre la recurrencia que calulemos anteriormente $F$ y las combinatorias binomiales. De hecho si rotamos 45 grados a la tabla inicial ¡obtenemos el triángulo de Pascal! Las recurrencias de las combinatorias son similares $\binom{x}{0}=\binom{x}{x}=1$, $\binom{x}{y}=\binom{x}{y-1} + \binom{x-1}{y}$.
1, 3, 5, 9, 17, 31, ?
Solución9 = 1 + 3 + 5
17 = 9 + 5 + 3
31 = 17 + 9 + 5
En la siguiente figura se muestra un rey en la casilla c2, y un círculo en f7
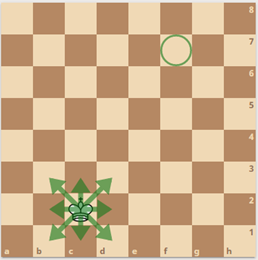
El rey se mueve como en el ajedrez. En un movimiento, puede moverse a cualquiera de las casillas adyacentes que comparta al menos un vértice con la casilla en la que está actualmente
¿Cuál es el mínimo número de movimientos necesarios para que el rey llegue hasta el círculo?
SoluciónEl rey debe dar 3 pasos en horizontal y 5 en vertical. Para acortar la distancia, al rey le conviene dar la máxima cantidad de pasos en diagonal. Un paso en diagonal es equivalente a dar un paso en horizontal seguido de uno en vertical. Por lo tanto, despues de 3 pasos en diagonal, solo le faltará dar dos pasos más en vertical. En matemática esta métrica es conocida como Distancia de Chebyshev.
Leonardo vive en un país de 5 ciudades (enumeradas desde 1 hasta 5). Por cada par de ciudades diferentes, existe una carretera que las conecta. La figura de abajo muestra un mapa del pais.
Leonardo está en la ciudad 1 y quiere viajar hasta la ciudad 4. Durante su viaje, Leonardo no quiere visitar la misma ciudad más de una vez.
Leonardo puede realizar su viaje de varias formas. Por ejemplo, puede ir directo hasta la ciudad 4, o seguir otra secuencia más larga como 1, 2, 5, 4.
¿De cuántas formas diferentes puede Leonardo realizar su viaje?

La figura de abajo muestra una región poligonal azul (histograma).
Un rectángulo es bueno si cumple las siguientes restricciones:
¿Cuántos rectángulos buenos existen con área máxima?
Más formalmente, sea S el conjunto de todas las áreas de rectángulos buenos, y sea A el máximo elemento de S (el número más grande). Calcula el número de rectangulos buenos con área igual a A.
SoluciónAlgunos participantes buscaban los cuadrados multiplicando base x altura, es más natural usar la definición de área i.e el número de cuadraditos de 1 x 1 que entran en la figura
La siguiente figura muestra uno de los rectángulos buenos de área máxima (8 cuadraditos)

Samuel y Feliza estan jugando con piedritas. Hay dos filas, la primera con 6 piedritas y la segunda con 4.
Samuel y Feliza alternan turnos, Samuel mueve primero, luego Feliza y así sucesivamente.
En cada turno el jugador que le toca puede seleccionar una de las filas y quitar un número positivo (mayor a cero) de piedritas.
El jugador que no pueda sacar piedritas pierde.
Antes de empezar el juego, Feliza eliminará algunas de las piedritas de cualquiera de las filas (quizas de ambas filas). Para que Samuel no sospeche, Feliza dejará al menos una piedrita en cada fila.
¿De cuántas formas puede Feliza eliminar las piedritas para garantizar su victoria?

| Usuario | Puntos |
|---|---|
| Juliaruiz1 | 30 |
| wil | 30 |
| AILE | 30 |